Bootstrapping In R (Linear Regression)
Bootstrapping is a method that can be used to estimate the standard error of any statistic and produce a confidence interval for the statistic.
The basic process for bootstrapping is as follows:
- Take k repeated samples with replacement from a given dataset.
- For each sample, calculate the statistic you’re interested in.
- This results in k different estimates for a given statistic, which you can then use to calculate the standard error of the statistic and create a confidence interval for the statistic.
set.seed(0)
library(boot)
#define function to calculate R-squared
rsq_function <- function(formula, data, indices) {
d <- data[indices,] #allows boot to select sample
fit <- lm(formula, data=d) #fit regression model
return(summary(fit)$r.square) #return R-squared of model
}
#perform bootstrapping with 10000 replications
reps <- boot(data=mtcars, statistic=rsq_function, R=10000, formula=mpg~disp)
#view results of boostrapping
reps
ORDINARY NONPARAMETRIC BOOTSTRAP
boot(data = mtcars, statistic = rsq_function, R = 10000, formula = mpg ~
disp)
Bootstrap Statistics :
original bias std. error
t1* 0.7183433 0.00285 0.06477
From the results we can see:
The estimated R-squared for this regression model is 0.7183433.
The standard error for this estimate is 0.06477.
We can quickly view the distribution of the bootstrapped samples as well:
plot(reps)
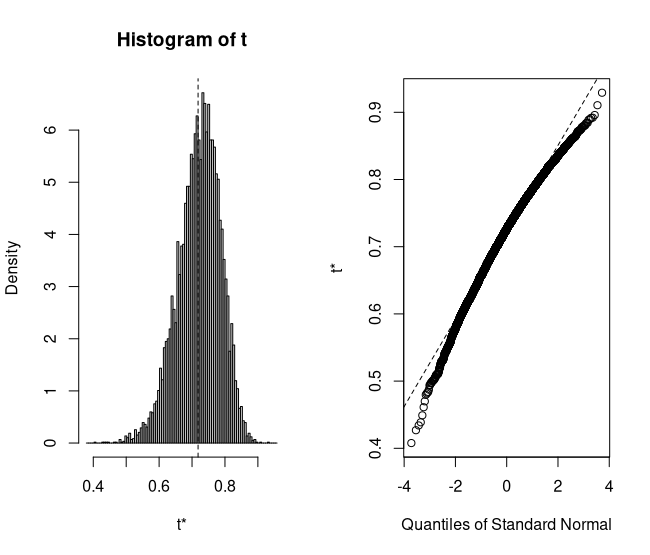
Now its time to bootstrap a linear model
# Generating data
set.seed(2021)
n <- 10000
x <- mtcars$mpg
y <- mtcars$hp
#Models of population and sample
population.data <- as.data.frame(cbind(x, y))
population.model <- lm(y ~ x, population.data)
summary(population.model)
#Sampling the data
sample.data <-
population.data[sample(nrow(population.data), 20, replace = TRUE), ]
sample.model <- lm(y ~ x, data = sample.data)
summary(sample.model)
#Plotting the models
plot(y ~ x, col = "black", lwd = 2, main = 'Population and Sample Regressions')
abline(coef(population.model)[1], coef(population.model)[2], col = "red")
abline(coef(sample.model)[1],
coef(sample.model)[2],
col = "blue",
lty = 2)
legend(
"topright",
legend = c("Sample", "Population"),
col = c("red", "blue"),
lty = 1:2,
cex = 0.8)
# The bootstrap regression
sample_coef_intercept <- NULL
sample_coef_x1 <- NULL
for (i in 1:10000) {
sample_d = sample.data[sample(1:nrow(sample.data), nrow(sample.data), replace = TRUE), ]
model_bootstrap <- lm(y ~ x, data = sample_d)
sample_coef_intercept <-
c(sample_coef_intercept, model_bootstrap$coefficients[1])
sample_coef_x1 <-
c(sample_coef_x1, model_bootstrap$coefficients[2])
}
coefs <- rbind(sample_coef_intercept, sample_coef_x1)
Combining the results in a table
means.boot = c(mean(sample_coef_intercept), mean(sample_coef_x1))
knitr::kable(round(
cbind(
population = coef(summary(population.model))[, 1],
sample = coef(summary(sample.model))[, 1],
bootstrap = means.boot),4),
"simple", caption = "Coefficients in different models")
confint(population.model)
confint(sample.model)
a <-
cbind(
quantile(sample_coef_intercept, prob = 0.1),
quantile(sample_coef_intercept, prob = 0.90))
b <-
cbind(quantile(sample_coef_x1, prob = 0.1),
quantile(sample_coef_x1, prob = 0.90))
c <-
round(cbind(
population = confint(population.model),
sample = confint(sample.model),
boot = rbind(a, b)), 4)
colnames(c) <- c("1 %", "90 %",
"1 %", "90 %",
"1 %", "90 %")
knitr::kable(rbind(
c('population',
'population',
'sample',
'sample',
'bootstrap',
'bootstrap'),c))
Predicting on new data
new.data = seq(min(x), max(x), by = 0.05)
conf_interval <-
predict(
sample.model,
newdata = data.frame(x = new.data),
interval = "confidence",
level = 0.90)
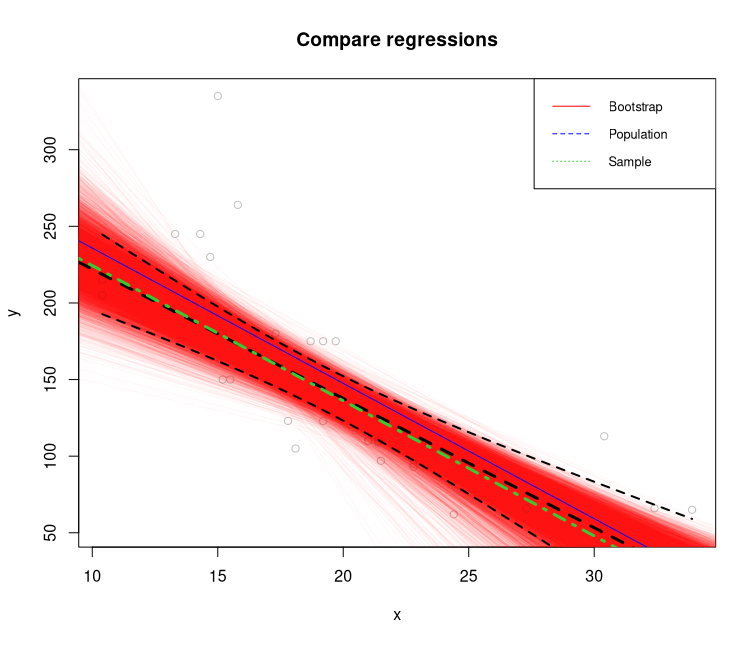
Plotting the results on the project step-by-step
plot(
y ~ x,
col = "gray",
xlab = "x",
ylab = "y",
main = "Compare regressions")
apply(coefs, 2, abline, col = rgb(1, 0, 0, 0.03))
abline(coef(population.model)[1], coef(population.model)[2], col = "blue")
abline(coef(sample.model)[1],
coef(sample.model)[2],
col = "black",
lty = 2, lwd=3)
abline(mean(sample_coef_intercept),
mean(sample_coef_x1),
col = "limegreen",
lty = 4, lwd=3)
lines(new.data, conf_interval[, 2], col = "black", lty = 2, lwd=2)
lines(new.data, conf_interval[, 3], col = "black", lty = 2, lwd=2)
legend("topright",
legend = c("Bootstrap", "Population", 'Sample'),
col = c("red", "blue", 'limegreen'),
lty = 1:3,
cex = 0.8)
Bootstrapping Plot